Hình thang còn được coi là một tứ giác lồi nhưng đặc biệt hơn bởi chúng có hai cạnh song song. Đây là một hình mà ta bắt gặp chúng khá nhiều trong cuộc sống hằng ngày. Hai cạnh song song của hình thang gọi là các cạnh đáy, các cạnh còn lại được gọi là cạnh bên. Nếu như việc tính chu vi hình thang có vẻ khá dễ nhớ, chỉ đơn giản là cộng tổng độ dài 4 cạnh thì cách tính diện tích hình thang lại khó ghi nhớ hơn một chút.
Cách tính diện tích hình thang
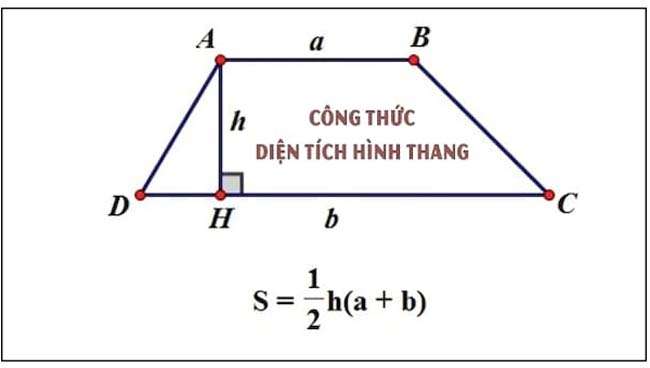
Khái niệm: Hình thang còn được coi là một tứ giác lồi có hai cạnh đáy song song, 2 cạnh còn lại không song song được gọi là hai cạnh bên.
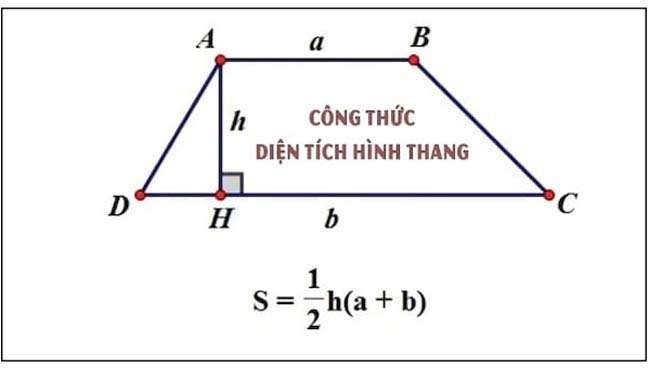
Tổng quát: Gọi các cạnh của hình thang là ABCD với độ dài đáy AB = a, đáy CD = b và chiều cao h.
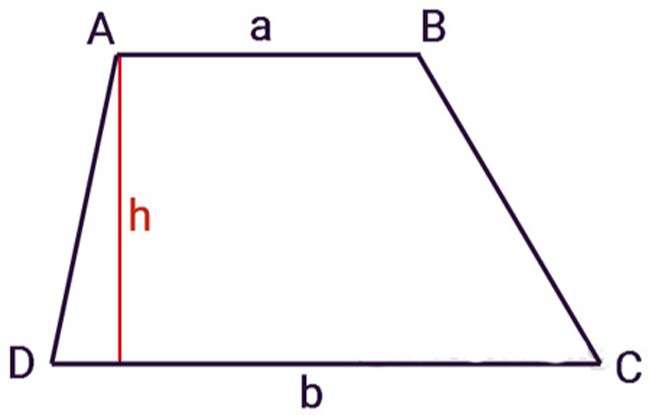
Công thức tính diện tích hình thang tổng quát:
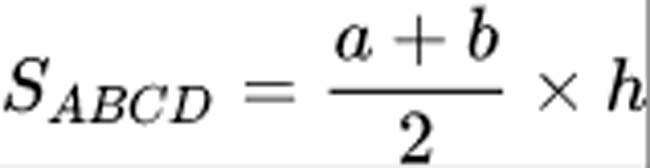
Trong đó:
- S = diện tích hình thang.
- a và b được coi là độ dài 2 cạnh đáy.
- h là chiều cao kéo từ cạnh đáy a xuống cạnh đáy b hoặc ngược lại (độ dài đoạn thẳng nối giữa 2 cạnh đáy).
Còn có bài thơ về cách tính diện tích hình thang khá dễ nhớ và được lưu truyền như sau:
Muốn tính diện tích hình thang
Đáy lớn đáy bé ta đem cộng vào
Thế rồi nhân với chiều cao
Chia đôi lấy nửa thế nào cũng ra
Ví dụ minh họa:
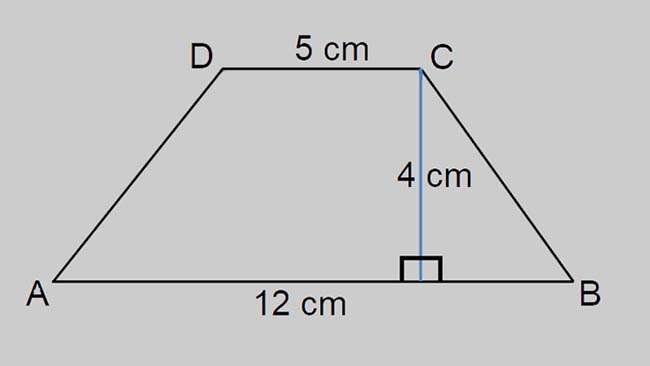
Một hình thang có chiều cao h = 4cm, đáy bé a = 5cm, đáy lớn b = 12cm. Tính diện tích hình thang đã cho?
Áp dụng công thức tính hình thang có diện tích như sau:
S = h x ((a +b) / 2) = 4 x ((5+12) / 2)= 34 (cm2).
Cách tính diện tích cho hình thang vuông
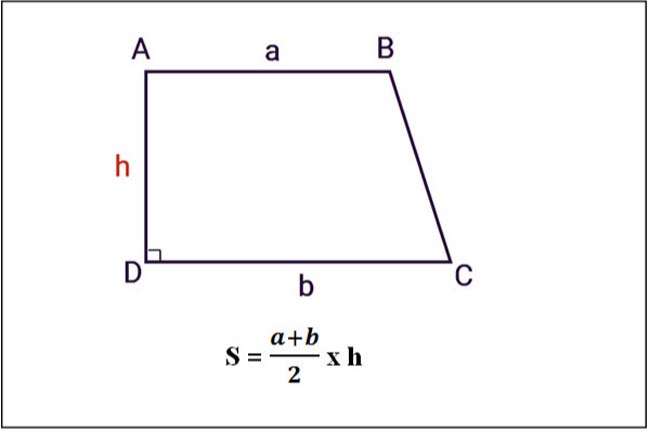
Hình thang có một góc vuông được tạo bởi 2 cạnh liền kề nhau gọi là hình thang vuông.
Hình thang vuông có cạnh bên vuông góc với hai đáy và cũng chính là chiều cao h của hình thang.
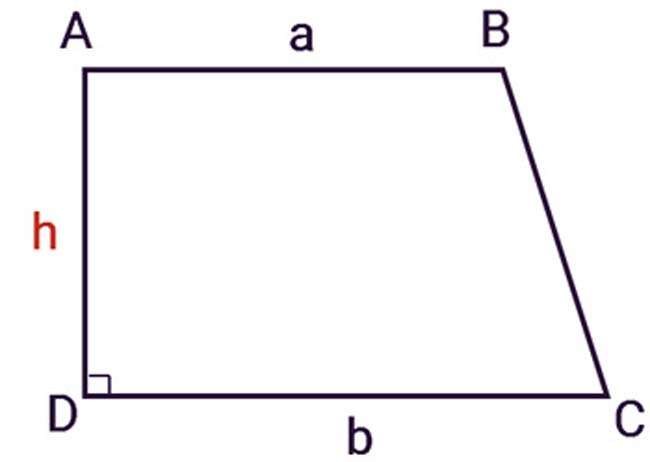
Công thức tổng quát tính diện tích hình thang vuông tương tự như công thức tính hình thang thường: trung bình cộng của 2 cạnh đáy nhân với độ dài của chiều cao giữa 2 đáy, tuy nhiên chiều cao h ở đây chính là cạnh bên vuông góc với cả 2 đáy của hình thang.
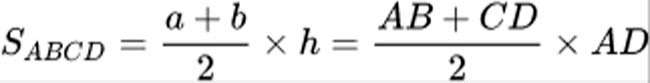
Trong đó:
- S = diện tích hình thang.
- a và b là chiều dài của 2 cạnh đáy.
- h = độ dài của cạnh bên vuông góc với 2 cạnh đáy.
Ví dụ minh họa:
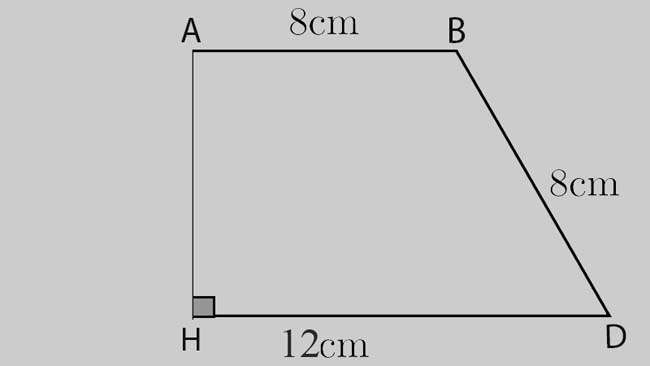
Một hình thang vuông ABHD có độ dài đáy bé và đáy lớn lần lượt là 8cm và 12cm. Trong đó có cạnh bên AH = 8cm. Hãy nêu công thức và tính diện tích của hình thang vuông đó.
Áp dụng công thức tổng quát đã cho phía trên, ta có:
S = h x ((a + b) / 2) = 8 x ((8 + 12) / 2) = 80cm.
Cách tính diện tích cho hình thang cân
Một hình thang có hai góc kề một đáy bằng nhau được gọi là hình thang cân. 2 cạnh bên của hình thang cân có độ dài bằng nhau và không song song với nhau.
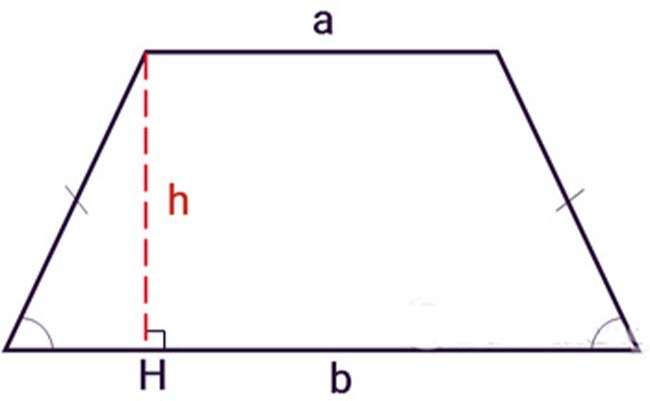
Ngoài việc áp dụng công thức tổng quát như công thức tính hình thang bình thường, bạn cũng có thể làm theo phương pháp sau: Chia nhỏ hình thang cân ra thành 2 tam giác và một hình chữ nhật sau đó tính diện tích từng phần rồi cộng lại với nhau.
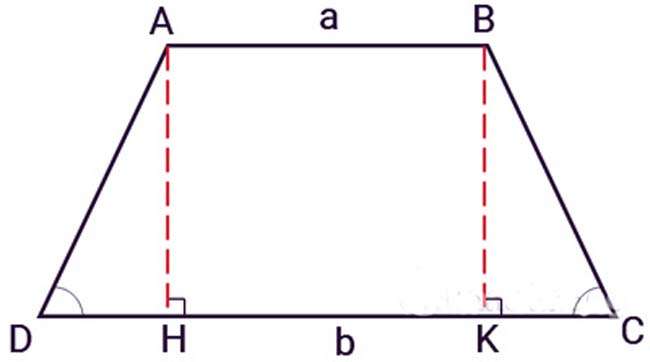
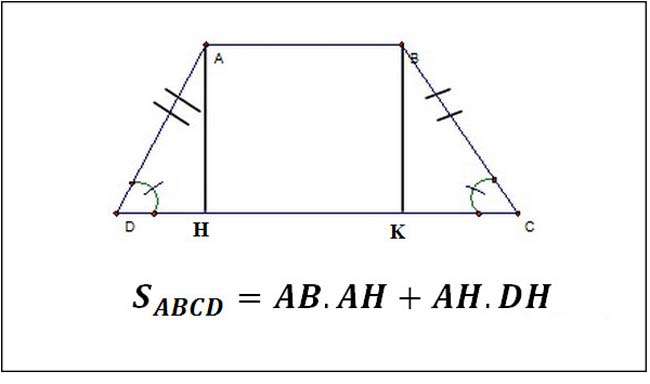
Giả dụ: Có hình thang cân ABCD: 2 cạnh bên AD và BC bằng nhau. Kẻ thêm đường cao AH và BK, hình thang sẽ được chia nhỏ ra thành 1 hình chữ nhật ABKH và 2 hình tam giác bằng nhau là ADH và BCK.
Áp dụng công thức tính diện tích cho hình chữ nhật cho ABHK và diện tích tam giác cho hình tam giác ADH và BCK sau đó cộng tất cả diện tích của 3 hình trên để tìm diện tích hình thang ABCD.
Cụ thể, phương pháp chia nhỏ này được thực hiện như sau:

Ví dụ minh họa:
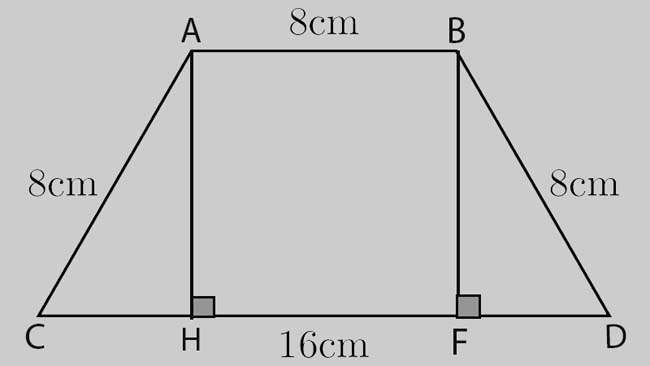
Cho hình thang vuông cân ABCD có: 2 cạnh đáy AB = 8cm, CD = 16cm. Hai cạnh bên bằng nhau và đều bằng 8 cm. Tính diện tích hình thang trên
Ví dụ minh họa cách tính phương pháp chia nhỏ để tính hình thang vuông cân
Áp dụng công thức ta có:
S = h x ((a + b) / 2) = 8 x ((8+16) / 2) = 96cm.
S = 2 x S của ACH + S của ABHF = 2 x 1/2 x 8 x 4 + 8 x 8 = 96cm.
Tính độ dài cạnh đáy của hình thang khi đã biết diện tích và chiều cao
Khi được cho trước diện tích, chiều cao và độ dài của 1 cạnh đáy, bạn có thể tính được độ dài cạnh đáy còn lại bằng công thức như sau:
AB= 2 x (S của ABCD / h) – CD
Tính diện tích của hình thang khi biết 4 cạnh
Cho hình thang ABCD biết: AB = a, BC = b, CD = c, DA = d.
Ta có công thức tổng quát để tính diện tích hình thang như sau:
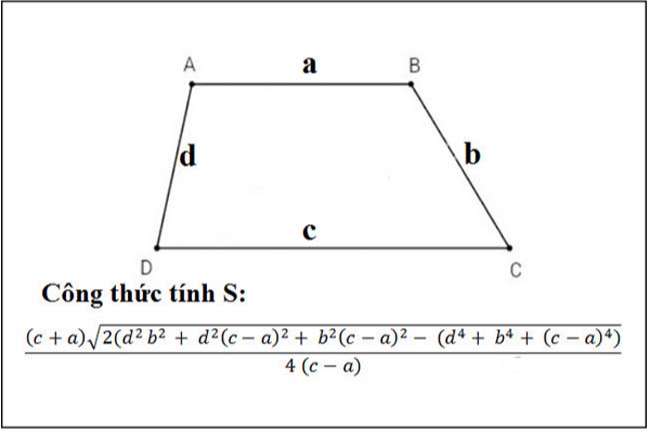
Thực tế, nếu bài toán đưa ra câu hỏi yêu cầu tính diện tích của hình thang khi biết 4 cạnh thì sẽ không tính được đáp án chính xác vì chỉ biết 4 cạnh thì có rất nhiều trường hợp xảy ra và diện tích cũng sẽ là khác nhau.
Ôn lại kiến thức
Kiến thức về hình thang hiện nay khá phổ biến với các bạn học sinh ở cấp 1. Để ôn lại các bài toán có nội dung liên quan tới công thức tính diện tích hình thang ta cần nắm rõ các khái niệm và các loại hình thang.
Trước hết ta cần nắm rõ khái niệm hình thang là gì? Hình thang còn được coi là tứ giác lồi có 2 cặp cạnh đối diện song song với nhau được gọi là 2 cạnh đáy, 2 cạnh đối diện còn lại gọi là 2 cạnh bên.
Các loại hình thang phổ biến gồm: Hình thang vuông (hình thang có 1 góc vuông, cạnh bên vuông góc với cạnh đáy), hình thang cân (hình thang có 2 cạnh đối diện bằng nhau và không song song với nhau), hình thang vuông cân (chính là hình chữ nhật).
Trên đây là tổng hợp thông tin chi tiết và các ví dụ minh họa cho cách tính diện tích hình thang. Hy vọng bài viết này sẽ đem lại cho bạn đọc những kiến thức bổ ích phục vụ cho việc học tập của mình.